Caesar Cipher Algorithm: Mathematical Formula and Implementation
Master Caesar cipher algorithm with mathematical formulas, multi-language implementations, complexity analysis, and optimization strategies for production-ready code.

The Caesar cipher stands as one of the most fundamental algorithms in computer science education, serving as an elegant introduction to cryptographic principles and mathematical computation. Named after Julius Caesar who used it for military communications around 50 BCE, this substitution cipher demonstrates core concepts that every computer science student must master: modular arithmetic, character encoding, and algorithmic complexity analysis.
Understanding the Caesar cipher algorithm provides essential foundation for grasping symmetric encryption systems, offering clear insight into how mathematical formulas translate into practical code implementations. This algorithm perfectly illustrates the relationship between theoretical mathematical principles and real-world programming applications, making it an invaluable learning tool for algorithm analysis and cryptographic understanding.
In this comprehensive guide, we'll explore the mathematical foundations underlying the Caesar cipher algorithm, examine its implementation across multiple programming languages, and analyze its computational complexity. We'll also discuss optimization strategies and advanced considerations that transform a simple educational exercise into a robust, production-ready implementation.
For beginners starting their cipher journey, check out our complete Caesar cipher tutorial for beginners before diving into the mathematical details below.
Quick Navigation: Jump to Mathematical Foundation, Implementation Examples, Complexity Analysis, or Advanced Considerations.
Caesar Cipher Mathematical Foundation
Caesar Cipher Mathematical Formula
The Caesar cipher operates on a beautifully simple mathematical principle using modular arithmetic. The fundamental encryption and decryption formulas form the algorithmic core:
Encryption Formula:
C = (P + K) mod n
Decryption Formula:
P = (C - K) mod n
Where:
- C: Ciphertext character (represented as numeric value)
- P: Plaintext character (represented as numeric value)
- K: Key (shift value, typically 1-25)
- n: Size of alphabet (26 for English)
The critical insight lies in handling negative modulo operations during decryption. Since many programming languages handle negative modulo differently, the safe decryption formula becomes:
P = (C - K + n) mod n
This ensures proper character wrapping regardless of the programming language's modulo implementation.

Caesar Cipher Modular Arithmetic
Modular arithmetic serves as the mathematical engine driving the Caesar cipher's character transformation. The modulo operation ensures that alphabet characters wrap around correctly: when 'Z' shifts forward, it becomes 'A', maintaining the closed alphabet system.
Let's work through some hands-on examples to see how the math actually works in practice:
Encryption Example:
- Character: H (position 7 in 0-indexed alphabet)
- Key: 3
- Calculation: (7 + 3) mod 26 = 10
- Result: K (character at position 10)
Wrap-around Example (this is where it gets interesting!):
- Character: Z (position 25)
- Key: 3
- Calculation: (25 + 3) mod 26 = 28 mod 26 = 2
- Result: C (character at position 2)
Pro Tip: The wrap-around is what makes Caesar cipher work! Without modular arithmetic, we'd run out of alphabet characters.
Decryption Example:
- Ciphertext: K (position 10)
- Key: 3
- Calculation: (10 - 3 + 26) mod 26 = 7
- Result: H (character at position 7)
Character Encoding in Caesar Cipher
The mathematical formulas work with numeric representations, requiring conversion between characters and alphabet indices. The standard approach uses ASCII arithmetic:
Character to Index Conversion:
index = char - 'A' // For uppercase letters
index = char - 'a' // For lowercase letters
Index to Character Conversion:
char = index + 'A' // For uppercase letters
char = index + 'a' // For lowercase letters
This encoding system preserves case information while enabling mathematical operations on character data. Non-alphabetic characters (spaces, punctuation) typically remain unchanged, maintaining text readability and structure.
Caesar Cipher Algorithm Design
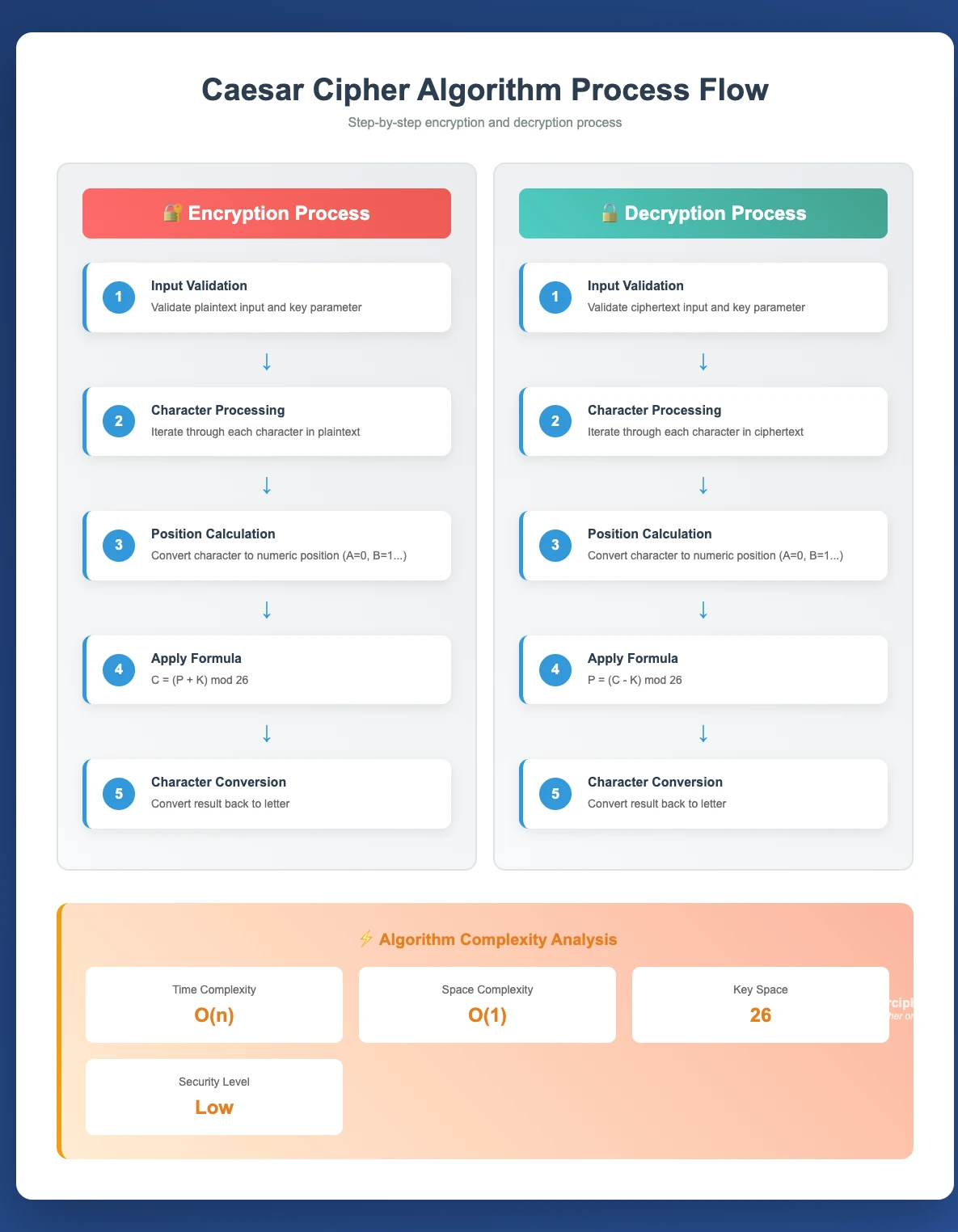
High-Level Algorithm Flow
The Caesar cipher algorithm follows a systematic approach that processes each character individually:
- Initialization: Set key value and alphabet parameters (typically n=26)
- Character Processing Loop:
- Examine each character in input text
- Determine if character is alphabetic
- Preserve non-alphabetic characters unchanged
- Alphabetic Character Transformation:
- Convert character to alphabet index (0-25 range)
- Apply mathematical shift formula with modular arithmetic
- Convert result back to character representation
- Preserve original case (uppercase/lowercase)
- Result Assembly: Combine transformed characters into output string
Detailed Pseudocode Implementation
Edge Cases and Error Handling
Robust implementations must address several edge cases:
Key Validation: Ensure key values are integers within reasonable ranges. Negative keys should be normalized: key = ((key % 26) + 26) % 26
Empty Input Handling: Return empty string for null or empty input without error
Unicode Considerations: Define behavior for non-ASCII characters (preserve unchanged or raise exception)
Memory Management: For large texts, consider streaming approaches to prevent memory overflow
Caesar Cipher Implementation Examples
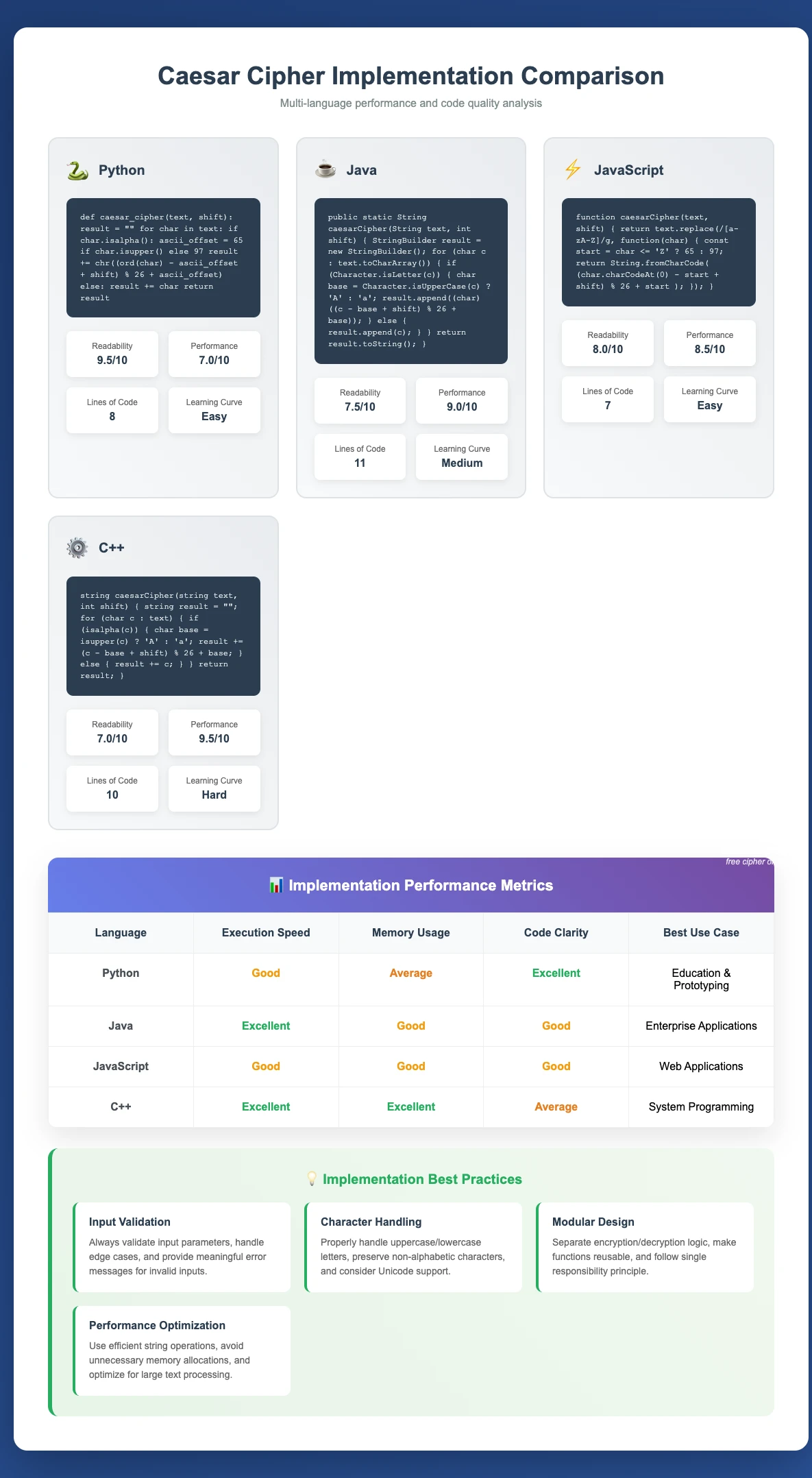
Python Implementation
Python's elegant syntax and built-in string methods make it ideal for demonstrating the algorithm clearly:
JavaScript Implementation
JavaScript's string manipulation capabilities provide clean implementation suitable for web applications:
Java Implementation
Java's strong typing system provides explicit algorithm structure ideal for educational analysis:
Caesar Cipher Complexity Analysis
Time Complexity Analysis
Here's something that might surprise you: the Caesar cipher demonstrates linear time complexity O(n) where n represents the input text length. This means whether you're encrypting "Hello" or an entire novel, the processing time scales predictably:
Best Case: O(n)
- Every character must be examined at least once
- No optimization can reduce below linear time
- Character processing requires constant time per operation
Average Case: O(n)
- Single pass through input string required
- Each character undergoes constant-time mathematical operations
- String concatenation optimized in modern implementations
Worst Case: O(n)
- Complexity remains linear regardless of input characteristics
- All characters require identical processing time
- No pathological inputs increase complexity beyond linear
Space Complexity Analysis
Standard Implementation: O(n)
- Output string requires storage proportional to input size
- Additional constant space for variables and loop counters
- Most practical implementations require result string storage
In-Place Optimization: O(1)
- Possible with mutable character arrays or string builders
- Modifies input directly without additional string storage
- Limited applicability due to immutable string requirements in many languages
Performance Characteristics
Mathematical Operations: Each character requires exactly one modular arithmetic operation, providing predictable performance regardless of key value or alphabet position.
Memory Access Pattern: Sequential character processing provides excellent cache locality, optimizing CPU cache utilization and memory bandwidth.
Scalability Analysis: Linear scaling ensures predictable performance for large documents. Processing 1MB text file requires exactly 1000x the time of 1KB file.

Advanced Caesar Cipher Implementation
Unicode and Internationalization
Modern applications require support for extended character sets beyond basic ASCII alphabet:
Security and Performance Enhancements
Constant-Time Implementation: Prevent timing attacks by ensuring consistent execution time regardless of input characteristics:
Testing and Validation Strategies
Comprehensive testing ensures algorithm correctness across all edge cases:
Frequently Asked Questions
What is the mathematical formula for Caesar cipher?
The Caesar cipher uses two main formulas:
- Encryption:
C = (P + K) mod n - Decryption:
P = (C - K + n) mod n
Where C is ciphertext, P is plaintext, K is the shift key, and n is alphabet size (26 for English).
How does modular arithmetic work in Caesar cipher?
Modular arithmetic ensures proper character wrapping. When you shift 'Z' by 1, it becomes 'A' because (25 + 1) mod 26 = 0, which corresponds to 'A'.
What is the time complexity of Caesar cipher algorithm?
Caesar cipher has O(n) linear time complexity, where n is the length of input text. Each character requires exactly one mathematical operation.
Can Caesar cipher handle Unicode characters?
Standard Caesar cipher works with ASCII letters only. However, you can extend it to Unicode by defining custom alphabets for different character sets.
Why use (C - K + n) mod n for decryption?
Adding 'n' before taking modulo prevents negative results in languages that handle negative modulo operations differently, ensuring consistent decryption across all platforms.
Conclusion
The Caesar cipher algorithm serves as an exceptional foundation for understanding cryptographic principles, mathematical computation, and algorithmic analysis. To explore more cipher variations, see our comprehensive substitution cipher comparison and learn about the differences between Caesar and Vigenère ciphers. Its elegant mathematical formulation using modular arithmetic provides clear insight into symmetric encryption systems while demonstrating practical programming implementation strategies.
Through our comprehensive analysis, we've explored the algorithm's mathematical foundations, examined implementations across multiple programming languages, and analyzed computational complexity characteristics. For practical application, explore our Python Caesar cipher programming tutorial and test your knowledge with practice problems and solutions. The Caesar cipher's O(n) time complexity and straightforward character-by-character processing make it an ideal algorithm for educational purposes and practical application development.
Key insights for computer science students include the importance of modular arithmetic in cryptographic systems, the relationship between mathematical formulas and code implementation, and optimization strategies that transform simple algorithms into robust, production-ready solutions. Understanding edge case handling, Unicode considerations, and comprehensive testing methodologies prepares students for advanced algorithm development.
The Caesar cipher's enduring educational value lies not in its cryptographic strength, but in its perfect demonstration of fundamental computer science principles: mathematical precision, algorithmic thinking, complexity analysis, and systematic problem-solving approaches that form the foundation for advanced cryptographic study and software development excellence.